Sommaire
- Le 6 Sigma et l'Excellence Opérationnelle. Juste du bon sens ?
- Combien de valeurs sont nécessaires pour avoir un échantillon représentatif ?
- Exploiter la donnée pour optimiser le pilotage d'un procédé
- Statistical modeling: The need for a reliable approach to improve process knowledge and understanding
- Bayesian approach in cosmetical research : Application to a meta-analysis on the anti-pigmenting effect of vitamin C
- Comparabilité, équivalence, similarité... Comment les statistiques peuvent nous aider à en faire la démonstration. Et bientôt la fin d'un "blind test" pour les autorités de santé et les industriels
- Le maintien du statut validé, une étape du cycle de validation
- Stratégie de validation des procédés et mise en application de l'Annexe 15 des BPF et des guidances FDA. Vérification continue des procédés (CPV)
“In God we trust, all others must bring data“(1), une citation souvent attribuée à Edwards DEMING (le créateur de la roue éponyme) ou Jack WELSH (l’emblématique PDG de General Electric dans les années 90), qui peut à elle seule, résumer l’esprit de la méthodologie 6 Sigma : piloter les processus par les données. Cependant, le 6 Sigma souffre de son appellation (la prononciation est difficile) et en plus fait appel des acronymes – DMAIC – et rôles (Green Belt, Black Belt, Champion) qui peuvent rendre cette méthodologie absconse voire à la limite de la “secte”.

Dans son rapport annuel de 2000(2), les dirigeants de General Electric (GE) précisent que “GE n’a pas uniquement réalisé son meilleur résultat jamais atteint, mais elle a eu le plus fort taux de croissance de son histoire […] grâce à la poursuite rigoureuse de quatre grandes initiatives : globalisation, services, qualité six sigma et digitalisation. Nous avons modifié non seulement notre environnement de travail et ce que nous vendons, mais aussi notre façon de travailler, de penser et de répondre à nos clients“.
Le 6 Sigma ne peut se résumer à du simple bon sens. Redécouvrons-le et comprenons comment il peut contribuer à une meilleure maitrise des procédés de fabrication.
1. L’histoire du 6 Sigma
1.1 L’artisanat : un mode de production ancestral
L’Excellence Opérationnelle ne nait pas avec Toyota et le Toyota Production System (TPS) ou bien encore avec Motorola et le 6 Sigma. C’est une longue évolution des méthodes de production qui permet à l’artisanat puis à l’industrie de continuellement progresser.
Jusqu’à la révolution industrielle du XIXème siècle, les sociétés occidentales sont à dominante agraire et artisanale. Pour produire un bien, schématiquement il faut avoir recours à un artisan (une ressource). Cette relation d’unicité (1 bien = 1 artisan) a pour avantage que chaque bien produit soit unique et corresponde exactement à la demande du client. Par contre, les volumes sont faibles et les coûts élevés : 1 bien = 1 coût, 2 biens = 2 coûts… Bien que contraint par la ressource jusqu’à l’arrivée de la mécanisation, la production artisanale améliore continuellement son organisation.
1.2 La Renaissance : les prémices de nouvelles méthodes de production
En Juillet 1574, le Roi de France Henri III rend visite à la cité de Venise. Le 24 Juillet, “…après une promenade incognito pour faire des achats, le roi se rend à l’arsenal. C’est le cœur de la puissance maritime (marchande comme militaire) de Venise qui met en sourdine sa frilosité naturelle et sa suspicion foncière pour présenter au souverain le secret de sa force : ses meilleurs arsenalotti (ces ouvriers qui réalisent l’exploit de monter une galère pendant le temps de la collation qui est offerte au roi) et son organisation incomparable faite d’efficacité et de réactivité“(3). Le Roi Henri III découvre alors une incroyable avancée dans la façon de produire : le travail séquentiel… qui de nos jours apparait si naturel.
Ces avancées spectaculaires dans la production continuent avec, à la fin du XVIIIème siècle, la mise en place du système Gribeauval dans l’artillerie française : “Je dois mes victoires à ce génie de Gribeauval“(4) déclare Napoléon 1er. Jean Baptiste de Gribeauval [1715-1789] est nommé premier inspecteur de l’artillerie française en 1776. Il entreprend la refonte complète de son organisation et “impose l’unicité des mesures dans toutes les provinces de France pour les fabrications d’armement, une vraie révolution à une époque où chaque région, et même chaque ville, dispose de ses propres mesures ! Chez les fondeurs et dans les arsenaux, il impose également l’interchangeabilité de toutes les pièces et accessoires entre eux, la définition chiffrée et normée d’un seuil de tolérance pour toutes les pièces usinées et un contrôle rigoureux des fabrications, effectué suivant un cahier des charges précis et grâce à des boîtes de contrôle contenant des gabarits communs à tous les arsenaux“(5). Le système Gribeauval repose sur deux principes : standardisation et mobilité des pièces.
1.3 La révolution industrielle de Ford et Taylor
Ces principes, l’inventeur Eli WHITNEY [1765 – 1825] les reprend et les popularise aux Etats-Unis à la fin du XVIIIème et début du XIXème siècle. Il invente une machine à égrener le coton : séparer la graine du coton de sa fibre, tâche fastidieuse et coûteuse traditionnellement effectuée manuellement par les esclaves dans le sud des Etats-Unis. Au-delà de l’avancée technologique, il propose un modèle de commercialisation innovant : Eli WHITNEY vend l’égreneuse en pièces détachées standards facile à assembler par l’acheteur. Les bases de la production en série sont posées : “faire que chaque pièce en soit si exactement semblable que toute pièce de l’un puisse être utilisé dans tout autre“. Frederick TAYLOR [1856 – 1915] s’inspire de ces avancées techniques dans la production qu’il formalise dans la décomposition du travail en tâches élémentaires à temps d’exécution déterminée. La rencontre avec Henry FORD [1863 – 1947] est déterminante. En combinant les travaux de Frederick TAYLOR avec le travail à la chaîne, la production passe du monde artisanal (faible volume et coûts élevés pour des produits à façon) à la production de masse (fort volume et coûts faibles pour des produits standards).
1.4 La naissance des probabilités et des statistiques
En parallèle de ces avancées techniques, les mathématiques connaissent également une révolution avec la naissance du calcul des probabilités ou la quantification du “hasard” (de l’arabe al zahr signifiant… le dé(6)). Luca PACCIOLI (religieux italien franciscain du XVème siècle, mathématicien et fondateur de la comptabilité en partie double [1445-1517]) pose le problème des partis dans son livre “Summa de arithmetica, geometria, de proportioni et de proportionalita” (Venise, 1494) : “A et B jouent à la balla [la balle au prisonnier]. Ils sont d’accord pour continuer jusqu’à ce que l’un d’eux ait gagné six tours. En fait, le jeu s’arrête quand A a cinq points et B trois points. Comment la mise de départ doit-elle être répartie ?“(7). Reformulée autrement, la question est : quelle décision prendre pour répartir la mise sachant que A a cinq points, B trois points et que le vainqueur est celui qui a six points ? Ce problème a été reprit par de nombreux mathématiciens italiens : Pacioli en 1494, Forestani en 1603, Calandri, Cardano en 1539, Tartaglia en 1556, Peverone en 1558, Pagani en 1591, et chez le français Gosselin en 1578(8). Mais surtout par Blaise PASCAL [1623-1668] et Pierre de FERMAT [≈1610 – 1665] qui lors de leur correspondance de l’été 1654 établissent le célèbre triangle de Pascal – ou loi binomiale – permettant de calculer la probabilité d’occurrence théorique d’un événement. Jacques BERNOULLI [1654-1705] continue dans cette voie avec la loi des grands nombres tiré de son expérience “l’urne de Bernoulli”. Il appréhende alors la probabilité d’occurrence réelle afin d’estimer l’incertitude : à partir d’observations de fréquence Jacques BERNOULLI estime la réalité.
Concrètement si j’extrais de l’urne plusieurs échantillon de billes noires et blanches, je peux alors estimer la proportion réelle de billes noires et blanches c’est-à-dire calculer “la probabilité que l’erreur entre une valeur observée et la valeur vraie se situe dans une limite donnée“(9). Abraham de Moivre (mathématicien français [1667 – 1754]) s’intéresse aux travaux de Blaise PASCAL et Pierre de FERMAT et plus particulièrement à “la convergence des variables aléatoires, sous l’optique suivante : dans quelle mesure peut-on être sûr que lorsque l’on lance un grand nombre de fois un dé, la fréquence observée d’apparition du nombre “six” tend vers la probabilité théorique ?“(10). Abraham de MOIVRE constate une dispersion des résultats autour de la moyenne dessinant une distribution en forme de cloche : la loi normale de Laplace-Gauss. Il nomme cette dispersion l’écart-type. “Cette mesure est d’une importance cruciale pour déterminer si un ensemble d’observations comprend un échantillon suffisamment représentatif de l’univers dont elles font partie“(11).
1.5 Motorola et la maitrise statistique des procédés
Cette approche de la prédiction par la dispersion non seulement révolutionne les mathématiques mais a également un impact crucial deux siècles plus tard dans la maitrise des procédés de fabrication. Walter A. Shewhart, un physicien américain [1891 – 1967] en charge de la Direction technique de Bell Telephone Laboratories, met en place des cartes de contrôles afin d’assurer la qualité des produits fabriqués à l’usine Hawthorne de Western Electric. Les résultats de ses travaux sont publiés en 1931 dans son livre “Economic Control of Quality of Manufactured Product“, une référence encore de nos jours pour la maitrise de procédés de fabrication. C’est la naissance de la gestion de la Qualité.
La production de masse révolutionne la manière de produire et surtout permet d’offrir au plus grand nombre des produits jusqu’alors inaccessibles ou bien réservés à une élite. Produire en masse, c’est bien, mais risqué : produire 1 000 000 véhicules similaires c’est prendre le risque de répéter 1 000 000 de fois la même erreur. Très rapidement, les industriels sont confrontés à des problèmes de qualité : les volumes produits augmentent… tout comme les erreurs. Les travaux de Walter A. Shewhart permettent d’apporter des outils pour maitriser les procédés de fabrication grâce aux statistiques, le plus connu étant le PDCA : Plan, Do, Check, Act ou roue de Shewhart.
Edwards DEMING [1900 – 1993] popularisera dans les années cinquante le PDCA auprès des industriels japonais. De nos jours le PDCA est plus connu comme “la roue de Deming” et est la pierre angulaire de la norme ISO9001:2015 pour les Systèmes de management de la qualité : “La version 2015 est plus orientée “résultats” que “moyens”. Certains documents ne sont plus exigés, tels que le manuel qualité ou les procédures systèmes. C’est désormais aux équipes de déterminer leurs propres moyens et outils de fonctionnement. C’est une opportunité pour gagner du temps et favoriser vos priorités. Les normes ISO 9001 et ISO 14001 adoptent une structure commune, organisée selon le PDCA (Plan-Do-Check-Act)“(12).
Bill SMITH [1929 – 1993], le Directeur Assurance Qualité de MOTOROLA, réussit la jonction entre les approches statistiques et la production à grandes échelles en créant le 6 Sigma, fortement inspiré par le Total Quality Management (TQM) de Toyota. Il convainc les dirigeants de Motorola de son approche statistique afin de réduire les défauts dans les lignes de production et donc d’accroître la qualité… et les résultats. Le principe est statistiquement simple. Pour des données distribuées selon une loi normale, le 6 Sigma considère que dans un intervalle de six écarts-type appliqués de part et d’autre de la moyenne, il y a 99,99966% des données(13) (voir illustration ci-contre). Autrement dit, si une ligne de production fabrique 1 000 000 de pièces et que son niveau de qualité est 6 Sigma, elle génèrera 3,4 défauts pour 1 000 000 de pièces produites… l’objectif que MOTORALA se fixe dans les années 80. Le 6 SIGMA est né.
1.6 La diffusion de la culture de l’Excellence Opérationnelle par General Electric
General Electric et son emblématique PDG Jack WELSH généralisent le 6 SIGMA durant les années 90 à l’ensemble des processus du conglomérat grâce à la démarche Change Acceleration Process (CAP) et l’équation d’efficacité du changement “E = Q x A” : l’efficacité (E) de toute initiative est égale au produit de la qualité (Q) de la technicité, de la stratégie et de l’acceptation (A) de cette stratégie par les parties prenantes. General Electric se focalise sur l’augmentation de l’acceptation afin de pérenniser son initiative en formant ses collaborateurs au 6 Sigma. Combinant le PDCA l’approche Change Acceleration Process, General Electric formalise son approche par la méthodologie DMAIC : Define, Measure, Analyze, Improve, Control (en français, Définir, Mesurer, Analyser, Améliorer et Piloter). Des niveaux sont créés (Green Belt, Black Belt et Master Black Belt) en fonction de la maitrise de la méthodologie. Ces “belts”, une fois formés, conduisent des projets de résolution de problème, forment d’autres “belts“, contribuent à l’amélioration de processus… une vraie politique d’Excellence Opérationnelle qui se diffuse à tous les niveaux de l’entreprise. Les résultats ne se font pas attendre comme indiqué dans le chapeau de cet article : dans son rapport annuel de 2000(14), les dirigeants de General Electric (GE) précisent que “GE n’a pas uniquement réalisé son meilleur résultat jamais atteint, mais elle a eu le plus fort taux de croissance de son histoire […] grâce à la poursuite rigoureuse de quatre grandes initiatives : globalisation, services, qualité 6 Sigma et digitalisation. Nous avons modifié non seulement notre environnement de travail et ce que nous vendons, mais aussi notre façon de travailler, de penser et de répondre à nos clients“.
Avec la maitrise statistique des procédés, l’approche empirique (pour chaque problème l’objectif est de trouver une solution) devient une approche scientifique : pour chaque problème l’objectif est de trouver les causes racines, qui se résume dans l’équation Y = f(X1, X2, X3,… Xn) + ε où :
- “Y” est l’unité qui issue du processus et livrée au client,
- “f” est le processus qui génère le “Y”,
- “(X1, X2, X3,… Xn)” sont les causes racines connues qui influencent le “f” et ont donc une relation de cause à effet avec le “Y”,
- “ε” est le bruit, c’est-à-dire ce qu’on ne peut expliquer.
Prenons l’exemple de la réalisation d’un gâteau au chocolat :
- “Y” est le gâteau au chocolat,
- “f” représente toutes les tâches à réaliser en suivant la recette,
- “(X1, X2, X3,… Xn)” sont la quantité de farine, de sucre, d’œufs, la durée de cuisson, la température du four…,
- “ε” est ce qui ne s’explique pas : “le meilleur gâteau c’est celui de ma grand-mère“.
Si vous contrôlez le gâteau à la sortie du four, vous pourrez dire s’il est bon ou mauvais… mais ce sera trop tard dans le cas où il est mauvais. Vous devrez en cuisiner un nouveau, en espérant que cette fois-ci il soit bon. Par contre, si vous savez que vous devez mettre entre 50 et 55 grammes de farine, 100 et 110 grammes de sucre, 100 et 105 grammes de beurre, 200 à 210 grammes de chocolat, 3 œufs et que la température du four doit être comprise entre 180°C et 185°C et la durée de cuisson entre 25 minutes et 30 minutes, alors vous aurez une très forte probabilité de réussir votre gâteau… à ε près. La sortie du processus (Y) est déterminée par les entrées (X) lorsque ε est petit. Par conséquent, si vous pilotez les X, vous pouvez alors prédire de manière fiable le Y.
2. Exemple d’application du 6 Sigma en industrie(15)
2.1 Pour chaque problème l’objectif est de trouver les causes racines
Un industriel fabrique des produits agro-alimentaires de consommation courante. Pour l’une de ses gammes de produits, ses clients remontent régulièrement des non conformités en termes de ressenti ou perception du produit consommé : il n’y a pas la saveur attendue. Cela se traduit par des produits détruits lorsque le défaut est détecté par l’usine et par des réclamations consommateurs dans le cas contraire. L’objectif est d’identifier la racine des causes permettant d’expliquer pourquoi le processus génère des produits défectueux (problème de saveur) et ainsi piloter la racine des causes (les Xs) afin de prédire de manière fiable la saveur (le Y) : sans méthodologie, autant chercher une aiguille dans une botte de foin. Afin d’éviter cet écueil, l’usine entame une démarche d’élimination du défaut constaté en lançant un projet de maitrise de la variabilité industrielle en s’appuyant sur la méthodologie 6 Sigma – DMAIC :
- Définir : exposer le problème, valider sa pertinence par rapport aux objectifs de l’entreprise, confirmer le potentiel de gain, construire une équipe projet.
- Mesurer : comprendre le processus associé, valider l’existence du problème (fiabilité de la mesure, performance), consolider l’équipe.
- Analyser : identifier les causes sources du problème, les confronter à la réalité terrain, valider avec les opérationnels leur impact sur le processus.
- Améliorer : favoriser l’émergence de solutions pour supprimer ou réduire significativement le problème.
- Piloter : s’assurer de la pérennité de la solution ainsi que de sa maitrise, établir des outils de pilotage, amener à l’adhésion l’ensemble des opérationnels concernés.
Les phases DEFINIR et MESURER explicitent et calculent le problème quantitativement en identifiant l’unité produite par le processus (le Y, ici la saveur) et les exigences du client, à savoir son objectif et sa tolérance. Si le Y ne respecte pas les exigences de saveur du client alors le problème est avéré. Le calcul du problème (ou calcul de performance du processus) confirme son existence en chiffre : nous passons du ressenti “à chaque fois ça ne marche pas“, aux faits “Lors des vingt dernières productions, quatorze n’ont pas respecté les exigences du client“. Ces deux étapes évitent de démarrer une résolution de problème… s’il n’y a pas de problème.
La phase ANALYSER recherche les racine des causes. Pour cela, une cartographie du processus est réalisée avec les opérateurs et affichée tout au long du projet dans une salle (cf. photo ci-dessous). Cette représentation visuelle invite les opérateurs à indiquer là où ils pensent qu’un paramètre peut influencer la saveur, les post-it verts sur la photo ci-contre. Soixante-quatre causes racines potentielles sont identifiées. Un plan de relevés de dix-sept mille données est alors mis en place sur une période de quatre mois.
Une fois ces données collectées, l’analyse statistique peut alors commencer. Une méthode de régression PLS (Partial Least Square) est alors utilisée afin d’évaluer la relation entre la réponse Y et les variables explicatives X (paramètres procédé à étudier) : Y = f(X1, X2, X3,… Xn) + ε. La régression PLS est particulièrement adaptée lorsque les variables explicatives X sont nombreuses et que certaines variables sont corrélées entre elles. Le principe de cette méthode est de construire un modèle entre la réponse Y et des variables latentes (chaque variable latente, appelée aussi composante, étant une combinaison linéaire des variables explicatives initiales). Les résultats de la modélisation permettent ensuite de mettre en évidence les variables latentes qui expliquent/impactent le plus la réponse Y. Cette méthode a permis de confirmer ou d’infirmer l’intuition des opérateurs et cinq racines des causes sont alors identifiées statistiquement.
2.2 Le pilotage du procédé de fabrication : les cartes de contrôle
La phase AMELIORER : passer de l’analyse statistique à la réalité industrielle. L’impact des cinq causes racines sur le Y (la saveur) est modélisé statistiquement. Cette modélisation permet de calculer les limites de tolérance, appelées également spécifications produit fini, ne devant pas être dépassées par la racine des causes afin que la saveur respecte les exigences du client. A partir de ces limites de tolérance, l’industriel peut établir également des spécifications industrielles plus exigeantes. En effet, les limites de tolérances délimitent la zone au-delà de laquelle le Y ne satisfera pas les exigences du client. Conserver celles-ci comme tel est risqué : si votre voiture a une largeur de 180 centimètres, vous ne construisez pas un garage de 180 centimètres de largeur mais d’au moins 240 centimètres.
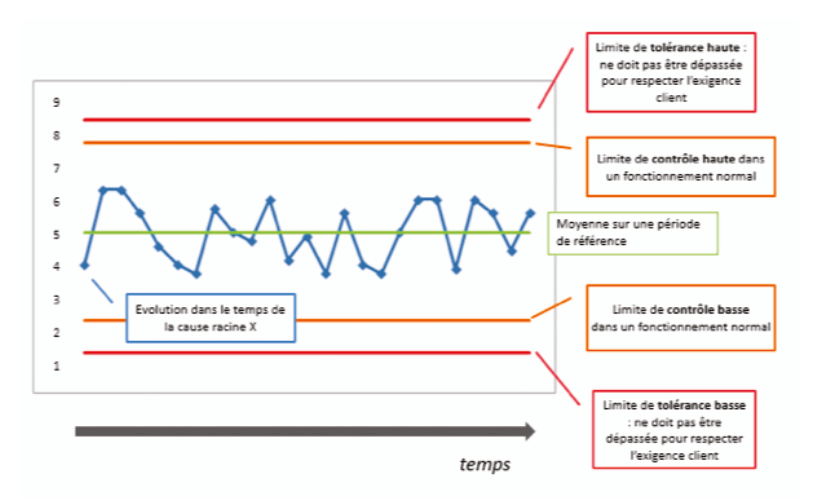
La phase PILOTER : de la réalité industrielle à l’application opérationnelle. Connaissant les limites à ne pas dépasser, tout l’enjeu est de s’assurer que la racine des causes respecte ces limites c’est à dire que sa variation est maitrisée afin de garantir la satisfaction client. La maitrise de cette variation ne passe pas uniquement par le respect des limites de tolérance ou spécifications industrielles mais principalement par la possibilité de détecter une tendance alertant sur un possible comportement anormal. C’est le principe des cartes de contrôle de Walter A. Shewhart vu précédemment : la maitrise statistique des procédés. Dans l’illustration ci-dessus, la cause source évolue dans une zone dite de contrôle et ne présente aucune tendance anormale : les données sont réparties normalement autour de la moyenne, en référence à la loi normale de Laplace-Gauss utilisée par Abraham de MOIVRE, et sont soumises uniquement à des causes communes c’est-à-dire propres au processus lui-même. Le processus est sous contrôle, l’opérateur est en capacité de piloter visuellement ce dernier.
Dans notre exemple, l’analyse des cinq racines des causes a permis de calculer les limites de tolérance, préciser des spécifications industrielles et calculer les limites de contrôles pour chaque racine des causes. La mise en place des cartes de contrôles directement sur les lignes de production permet aux opérateurs de prédire le défaut… et donc l’éviter.
3. Le 6 Sigma, une analogie avec le management
Le 6 Sigma est souvent associé aux statistiques, ce qui est vrai car elles y sont très prégnantes. Parfois, il n’est pas facile de les comprendre : réaliser un plan d’expérience ou conduire une analyse de variance (ANOVA) demande de bonnes connaissances sur le contexte d’utilisation de ces méthodes, ainsi que sur la manière d’interpréter les résultats.
Cependant, réduire le 6 Sigma aux outils statistiques, c’est croire qu’à tout problème il y a une solution technique unique. Une relation d’unicité un peu réductrice : “on a trouvé la solution, il n’y a qu’à dire aux équipes de l’appliquer“.
Pourquoi cherche-t-on à résoudre un problème ? Pour avoir un effet sur la satisfaction du client, la performance du processus, l’efficience de la réalisation etc… Une bonne solution technique y contribuera certainement…si elle est appliquée. En d’autres termes si les équipes n’utilisent pas la solution, cela n’a servi à rien de la chercher.
Le 6 Sigma est plus qu’une boite à outils pour résoudre des problèmes. Il n’apporte pas de solution “miracle“. Il recherche la racine des causes du problème, la met sous contrôle par un pilotage opérationnel et évite ainsi que le problème ne se reproduise. Dans l’exemple précédent, l’industriel n’a pas de solution “miracle“. Par contre les opérateurs connaissent les paramètres (racines des causes) qui influencent sur le processus. Ils ont les moyens de les piloter (les cartes de contrôles) et sont donc capables de maitriser le processus afin de délivrer le bon produit / service au client. Cette combinaison du “Comment” (la solution) et du “Pourquoi” (la cause) permet d’augmenter l’impact de l’effet recherché. Il est la combinaison de la qualité technique de la solution et de l’acceptation de cette même solution : EFFET = QUALITE X ACCEPTATION. En implémentant les cartes de contrôles (une maitrise chiffrée du processus), l’industriel de notre exemple a travaillé sur l’acceptation afin de garantir la saveur attendue par ses clients. “In God we trust, all others must bring data“(16).
Partager l’article

Damien BONHOMME – 3CONSEILS
damien.bonhomme@3conseils.com
Références
(1) En Dieu nous avons confiance, tous les autres doivent apporter des données
(2) GE Annual Report 2000 – page 4 – http://www.ge.com/annual00/download/images/GEannual00.pdf
(3) Marie Viallon. Les honneurs de Venise à Henri de Valois, roi de France et de Pologne : Etude du séjour vénitien du roi Henri III en 1574. Congrès annuel de la RSA, Apr 2010, Venise, Italie.
(4) “Gribeauval ou les débuts de la standardisation industrielle” – TRISTAN GASTON-BRETON HISTORIEN D’ENTREPRISE – LES ECHOS | LE 03/08/2016
(5) “Gribeauval ou les débuts de la standardisation industrielle” – TRISTAN GASTON-BRETON HISTORIEN D’ENTREPRISE – LES ECHOS | LE 03/08/2016
(6) “Against the Gods – the remarkable story of risk” de Peter L. Bernstein – 1996 – Edition Wiley p. 13
(7) “Against the Gods – the remarkable story of risk” de Peter L. Bernstein – 1996 – Edition Wiley p. 43
(8) LE PROBLÈME DES PARTIS BOUGE… DE PLUS EN PLUS – Norbert Meusnier – Université de Paris VIII – Electronic Journal for History of Probability and Statistics Vol 3 N°1 Juin 2007 – page 4
(9) “Against the Gods – the remarkable story of risk” de Peter L. Bernstein – 1996 – Edition Wiley p. 125
(10) Biographie d’Abraham de MOIVRE : http://www.bibmath.net/bios/index.php?action=affiche&quoi=demoivre
(11) “Against the Gods – the remarkable story of risk” de Peter L. Bernstein – 1996 – Edition Wiley p. 127-128
(12) AFNOR Certification “Guide de transition ISO9001 :2015 pour les petites et très petites entreprises” – novembre 2016
(13) Durant la vie d’un processus surviendra un décentrage (appelé “shift” en anglais) qui est estimé à 1,5 Sigma. On parle alors d’un Sigma long terme (LT) Vs un Sigma court terme (CT) où Sigma LT = Sigma CT – 1,5. Pour plus de précisions cf. “Six Sigma : comment l’appliquer” de Maurice PILLET / Eyrolles Août 2013 / Page 135
(14) GE Annual Report 2000 – page 4 – http://www.ge.com/annual00/download/images/GEannual00.pdf
(15) Les noms, chiffres et résultats ont été modifiés
(16) En Dieu nous avons confiance, tous les autres doivent apporter des données
Bibliographie
“Against the Gods: The Remarkable Story of Risk” de Peter L. Bernstein – John Wiley & Sons / 29 septembre 1998
“The Machine That Changed the World: The Story of Lean Production- Toyota’s Secret Weapon in the Global Car Wars That Is Now Revolutionizing World Industry” de James P. Womack, Dan T. Jones et Daniel Roos – Free Press / 13 mars 2007
“Economic control of quality of manufactured product” de Walter A. Shewhart – Martino Fine Books / 25 avril 2015
“Six Sigma : Comment l’appliquer” de Maurice Pillet – Eyrolles / 29 août 2013